How can I solve this recurrence :
f(n) = f((3/4)n) + f(n^(1-b)) + c n^b
where b and c are constants and 0<b<1 and f(1)=1
How can I solve this recurrence :
f(n) = f((3/4)n) + f(n^(1-b)) + c n^b
where b and c are constants and 0<b<1 and f(1)=1
Copyright © 2021 Jogjafile Inc.

We cannot directly use Akra-Bazzi theorem as you have mentioned, because we cannot write in the form of
in the form of
) such that
such that
 and
and
&space;=&space;O%5Cleft(%5Cfrac%7Bn%7D%7Blog(n)%5E2%7D%5Cright)) which is required for utilizing the theorem. However, we can find an upper bound by substituting
which is required for utilizing the theorem. However, we can find an upper bound by substituting
) with
with
) such that
such that
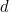 is constant and less than
is constant and less than
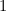 .
Now, we can use akra-bazzi theorem for
.
Now, we can use akra-bazzi theorem for
&space;=&space;f(%5Cfrac%7B3%7D%7B4%7D&space;n)&space;+&space;f(d%5Ctimes&space;n)&space;+&space;c&space;n%5Eb) .
To continue, first we need to solve
.
To continue, first we need to solve
 in the following equation:
in the following equation:
As we know in the integral part we have ,
if we choose
,
if we choose
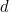 such that
such that
 ,
the upper bound is
,
the upper bound is
)) .
.
Hence, we can choose%5Eb%5Cright)%5E%7B%5Cfrac%7B1%7D%7Bb%7D%7D) which is less than
which is less than
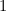 and a constant.
and a constant.